利息計算
|
|
数式 / 関数 |
知人から利率・借入額・年数から返済の額を算出してくれ。という依頼がありました。
そういう電卓や、計算してくれるサイトは多々あるかと思いますが、Excelで作ってみます。
ただ借入金の返済方法には主に3つの方法があります。
- 元利均等返済方式
- 元金均等返済方式
- アドオン方式
返済方法にも触れてみたいと思います。
各返済方法の計算式は・・・?
まずはこの計算式が解らないと作れませんのでそこの説明から。
元利均等返済方式
上図のように毎月の返済金額(元金+利息)を均等にした方式。ローンで最も普及した返済方式。裁判所の調停では,一般に,この返済方式が用いられています。
【メリット】
・ 毎回の返済額が一定で,返済計画が立てやすい。
・ 返済するにつれ,元本が増加,利息減少。
・ 元金均等返済に比し,当初返済額が少なくて済む。
【デメリット】
・ 元金均等返済に比し,総返済額が多くなる。
【計算式(毎月の返済金額)】
(借入金額 × 月利) ÷ (1 - (1 + 月利)-返済回数
※月利は年利÷12です。
元金均等返済方式
毎回の元金の返済額を均等にした返済方式
【メリット】
・ 毎回確実に均一に元金部分が減少,これにつれ利息も逓減。
・ 元利均等返済に比し,総返済額が少なくてすむ。
【デメリット】
・ 当初の返済額が多くなる。収入が多くないと借りにくい。
【計算式(毎月の返済金額)】
(借入金額 ÷ 返済回数) × (1 + (返済回数 - 計算対象月 + 1) × 月利)
※月々同額の支払いとならない。元金は一定だが利息が変わる為。
アドオン方式
毎回の返済額が一定で,しかも,利息計算の際,元本の減少を認めない方式。
割賦販売商品の代金返済,少額の消費者金融等に適用されている。
【メリット】
・ 毎回の返済額が均一で,計算が簡単。返済計画が立てやすい。
【デメリット】
・ 返済終了時点まで当初元本に対する利息を付すので,実質金利は高い。
・ 実質金利月利は,元利均等返済方式よる月利より,大体1.4~1.9倍多いといわれている。
【計算方法(毎月の返済金額)】
(借入金額 × (1 + 月利 × 返済月数)) ÷ 返済月数
じゃあExcelでどうすんの
うだうだと金利について説明しましたが本題です。Excelでどうやって作るのか。
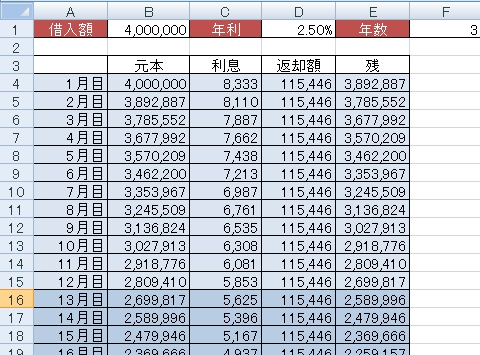
まずこの表を見てください。一般的なローン返済方法、元利均等返済方式を使っています。

上でも載せましたが、これを使って説明していきます。
B1の借入額、D1の年利、F1の年数は可変としています。
①月目の元金は当然借入額そのまま「=B1」ですね。
では①月目の利息は・・・というと
「=B4 * (D1 / 12)」
と、元金に月利を掛けたものになります。
①月目の返却額は上記の計算式を使って・・・
「=(B1 * (D1 / 12)) / (1 – (1 + (D1 / 12)) ^ -(F1 * 12))」
となります。
Excelで乗数を使う場合は「^」を使います。
元金+利息-支払額=その月の元金残
これを月々計算を繰り返すと36ヶ月後には残が0となるわけです。
ちなみに小数点以下の四捨五入はお忘れなく。。
もっと利息計算について詳しく知りたい場合はこちら
次回[ボタンで返済方法を切り替える]
関連記事
- 前の記事
- Excel2003でSUMIFSを実現
- 次の記事
- セルにデータバー(グラフ)を表示する













Comment
長文ですみません。
15年ほど前、今思えばカード破綻ぎりぎりでした。
まわすために、そのカード会社のキャッシングに頼るというような悪循環。
しかし、多少景気がよく、残業代で何とか息をついていました。
それがある日、突然の残業カット。 半年ほど不安な日々が続きました。
残業代が復活後、この苦しみから1ヶ月でも早く抜け出そうと、1か月分多く入金することにしました。
すると、後日送られてきた残金明細は、2.5か月分ほど減っているのです。
「これが複利の力なのか!」と、それからは残業代すべて返済に充てました。
確か6ヶ月か7ヶ月で完済しました。
もう少し利口だたらなあと、身をもって学びました。